今回は前回(k空間の充填方法)で解説できなかった部分についてまとめていきます。
各問題についての解説はして行きますがk空間の概要については省かせていただきます。
過去からの出題
第5回-20
第5回-20
Parallel Imaging について、正しい文章を解答して下さい。
a. SENSEの展開アルゴリズムはk空間上のデータに対して行われる。
解答
a.×画像上
パラレルイメージングは撮像時間を短縮させる技術ですが大きくSENSとSMASHに分けられます。
SENSEではk空間の位相エンコードステップを間引いて信号を取得、その分小さくなったFOVで折り返しが発生しますがコイルの感度差を利用して折り返しを戻して画像を作成する方法です。よって展開アルゴリズムは画像上で行われていることとなります。
SMASHではまず各コイルの空間感度分布を測定しそれら感度分布の合成を作成します。k空間の位相エンコードステップを間引いてスキャンし間引いたステップは合成感度分布で信号を算出し画像を作成します。こちらはk空間上で行われることとなります。
僕は『うちの中でスマブラをやる』と覚えました。ダサいですね。
うち→k空間内、スマブラ→SMASH
第6回-16
第6回-16
次の記述で、正しい文章を選択して下さい。(正解3つ)
1.k空間の座標軸は波数である。
2.SE 法では1つの MRI 信号が k 空間の1行を埋める。
3.実空間と k 空間は互いにフーリエ変換の関係にある。
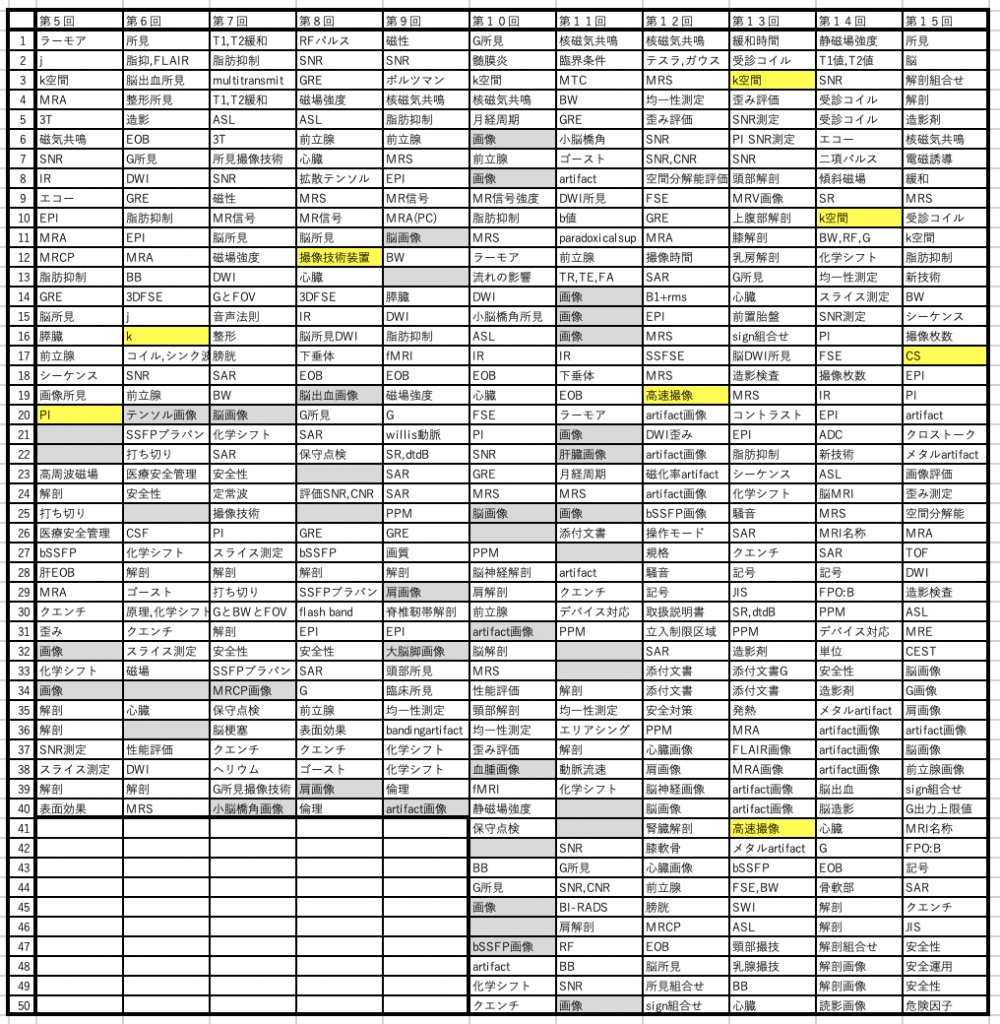
4.実空間の位置(座標)と k 空間の位置は同じである。
5.k空間を構成する各行の MRI 信号の強弱は周波数エンコード傾斜磁場の強さだけに影響される。
解答
a.○あるいは空間周波数
b.○1TR、位相エンコード1行を埋めることとなり全部で位相エンコード数分この作業を行います。
c.○被写体に磁場勾配を印加して信号取得するとフーリエ変換された状態でk空間に埋められます。それを逆フーリエ変換することで実画像となります。
d.×実空間の一部はk空間の全てから、同じくk空間の一部は実空間の全てから出来ています。実空間の右端がk空間の右端のような位置関係はありません。
e.×位相エンコード傾斜磁場の強さによります。
第8回-12
第8回-12
次の記述について正しい文章を選択してください。
1.radial scan は、k 空間における軌跡が放射状であり、3D 高速撮像で利用できない。
4.spiral scanとSSFPシーケンスと組み合わせることで更にSNRが向上し、現在心臓 MRI で頻用されている。
5.spiral scan は、k 空間における軌跡がスパイラル(渦巻き)であり、parallel imagingを併用することでさらに高速撮像化できる。
解答
1.×可能 3D Radial VIBE(シーメンス) ではモーションアーチファクトに強くかつ高分解能の撮像ができます。
4.× 心臓領域ではSSFPもspiral scanも用いられていますが併用するものなのかは不明。spiral scanではBBと併用しspiral-BBとして血管内膜の観察に使用されています。
5.○と思います。
第12回-19
第12回-19
高速イメージング技術について正しい文章を選択して下さい。(正解 2 つ)
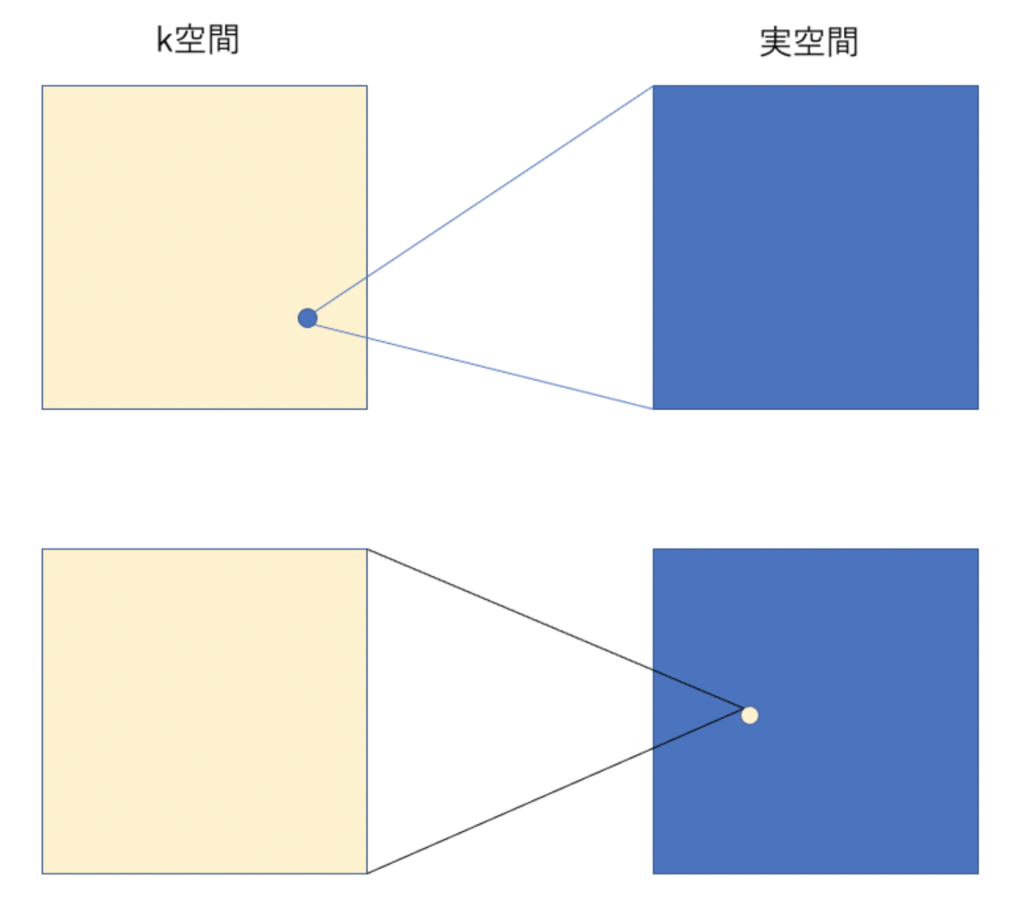
- スパイラルスキャンの信号取得 k 空間座標は極座標系である。
- 圧縮センシングは収集データから少数サンプリングによって画像を圧縮する方法である。
- SENSE(sensitivity encoding)法を用いた場合、SNR は用いない場合の √R(reduction factor)倍となる。
- Parallel imaging は k 空間を間引いて信号を取得し、複数コイルの空間的な感度差を利用して画像を作成する。
- SMASH(simultaneous acquisition of spatial harmonics)法はフーリエ変換後に折り返しを展開する方法である。
1.○螺旋状にスキャンするため極座標となります。
2.×多くの圧縮技術は大容量の観測データを取得後圧縮するが、圧縮センシングはスパース性を利用し観測データを少なくしk空間でのランダムサンプリングから圧縮を行います。
3.× S/NSENSE=(S/Nfull)/(g√R)
4.○です。
5.×フーリエ変換後にコイル感度差により折り返しを戻すのがSENSE。SMASHはk空間内での展開のためフーリエ変換前です。
第13回-3
第13回-3
k 空間に関する正しい記述はどれか。(正解 2 つ)
1. k 空間は複素数で表される。
2. 波数とは周波数の逆数である。
3. k 空間の中心は交流成分を意味する。
4. 空間周波数の単位は K(Kayser)で表される。
5. 位相エンコード数を少なくすると撮像時間は長くなる。
解答
1.○k空間は実部と虚部による複素数からできています。例)a+bi
2.×周波数:単位時間あたりの波の数〔Hz=s-1〕波数(空間周波数):単位距離あたりの波の数〔m-1〕
3.×交流とは関係ないと思います。
4.○ただし、絶対温度のケルビンKと区別するため正確には小文字のkを用いることとなっています。実際試験で出題されたら不正解かなと疑いたくなりますね。ちなみにカイザーとはドイツの分光学者だそうです。
5.×短くなります。撮像時間=TR×Ny×NSA
第13回-41
第13回-41
第12回-19と同じ問題
第14回-10
第14回-10
正しい記述はどれか。2つ選べ。
- 部分フーリエ法は撮像時間を短縮できる。
- ゼロ充填補間法は空間分解能が向上する。
- 実空間の位置(座標)は k 空間の位置に対応している。
- 実空間のピクセル径(Δ X)の逆数が k 空間の横軸の長さ(kx)になる。
- k 空間の空間周波数成分(Δ kx)の逆数が実空間のピクセル径(Δ X)になる。
解答
1.○k空間の充填方法、位相エンコード方向の約半分を実測し残りは補正値で埋める方法です。
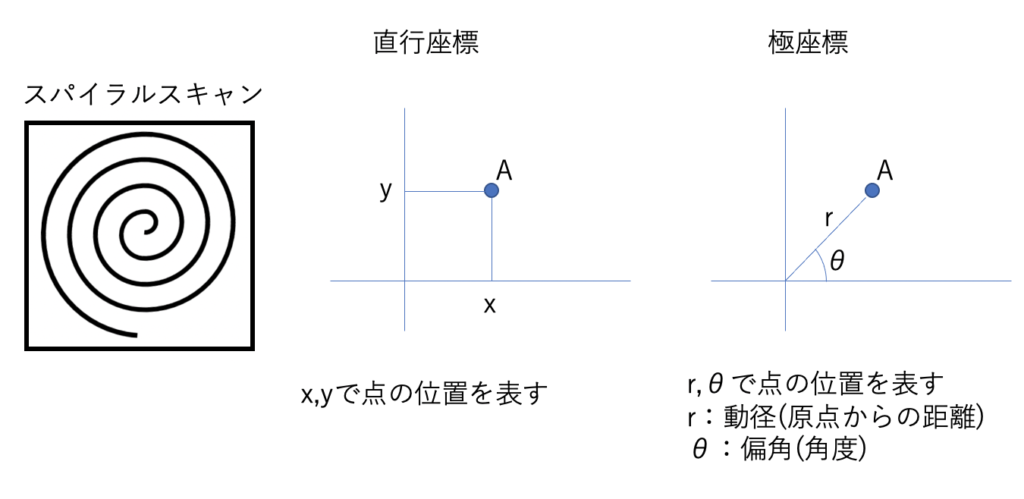
2.×ZIP(zero fill interpolation processing):実空間のピクセルはk空間の大きさ(LOK)と反比例するので、LOKを大きくするとピクセルは細かくなる、そこで実際には取得してないがk空間の行や列を0で充填し無理やりLOKを大きくしピクセルを細かくする方法、空間分解能は向上するがSNが下がったりボケが生じるので見かけの空間分解能の向上と言われる、消去法で×
3.×k空間の全てに対応
4.○です。
5.×です。(Δ kx)はFOVと(Δ X)はLOKと対応しています。k空間について
第15回-17
第15回-17
Compressed sensing MRI に関する正しい記述はどれか。2つ選べ。
- 収集データを間引いて画像を圧縮する方法である。
- k 空間をコヒーレント(coherent)にサンプリングする。
- MRA や MRCP といったコントラストの高い画像に有用である。
- ラジアル法やスパイラル法などの非直交座標系にも応用できる。
- スパース性が高いとは画像におけるゼロ成分が少ないことである。
解答
1.×スパース性を利用し観測データを少なくしk空間でのランダムサンプリングから圧縮を行います。
2.×インコヒーレント(でたらめに)
3.○白と黒がはっきりしスパースな(スカスカな)画像に有用です。
4.○応用技術にGRASPなどがあります。
5.×ゼロ成分が多いことです。
まとめ
問題に入る前にk空間について解説していこうと思いましたが長くなってきて断念しました。
k空間の記事はいくつかありますがきちんと解説したことはなかったので改めて記事にします。
k空間の出題は充填方法やk空間の特徴、パラレルイメージングのような技術など出題の幅が広くカバーしていくのは大変かもしれません。
まずは過去問だけでも理解できればと思います。
出題
第5回-20,第6回-16,第8回-12,第12回-19,第13回-3,第13回-41,第14回-10,第15回-17
参考書籍
MRI完全解説 P150
MRIの基本パワーテキスト P150











コメント