初歩の初歩、ラーモアの方程式について
ラーモア方程式
プロトンは磁場があってもなくても自転しています。
磁場環境にプロトンをおくと自転だけでなく、磁場の軸に対しても回り歳差運動を始めます。
この時の歳差運動をする速さ(ω)はラーモアの方程式で表すことができるのです。
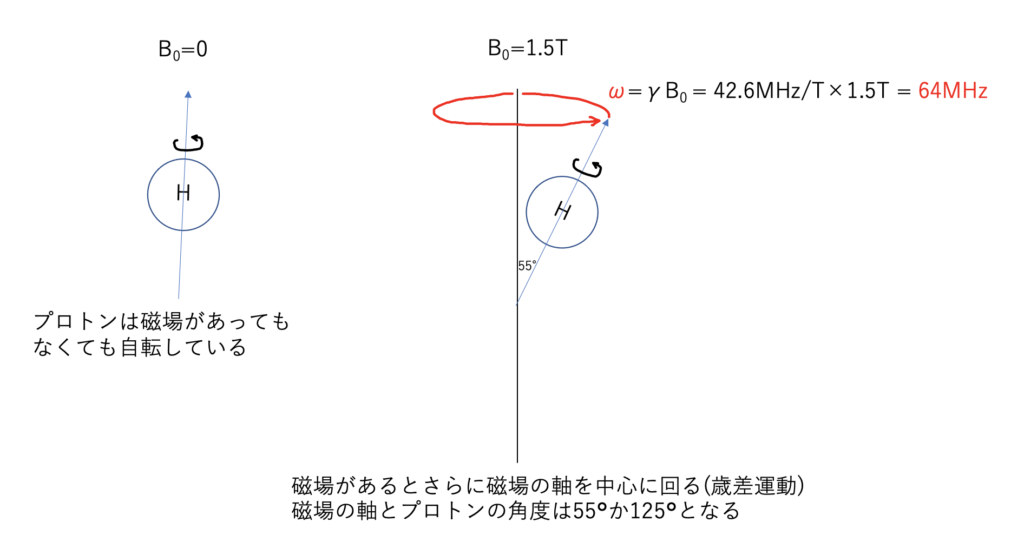
ラーモアの方程式はω=γB0
γは磁気回転比といい、核種によって異なる値です。プロトンの場合は42.6MHz/T
B0は静磁場で今回は1.5Tとします。
ω=γB0=42.6MHz/T×1.5T=64MHz となります。
このラーモアの方程式から導出された角周波数ωはプロトンを共鳴させるためのRFパルスとなります。
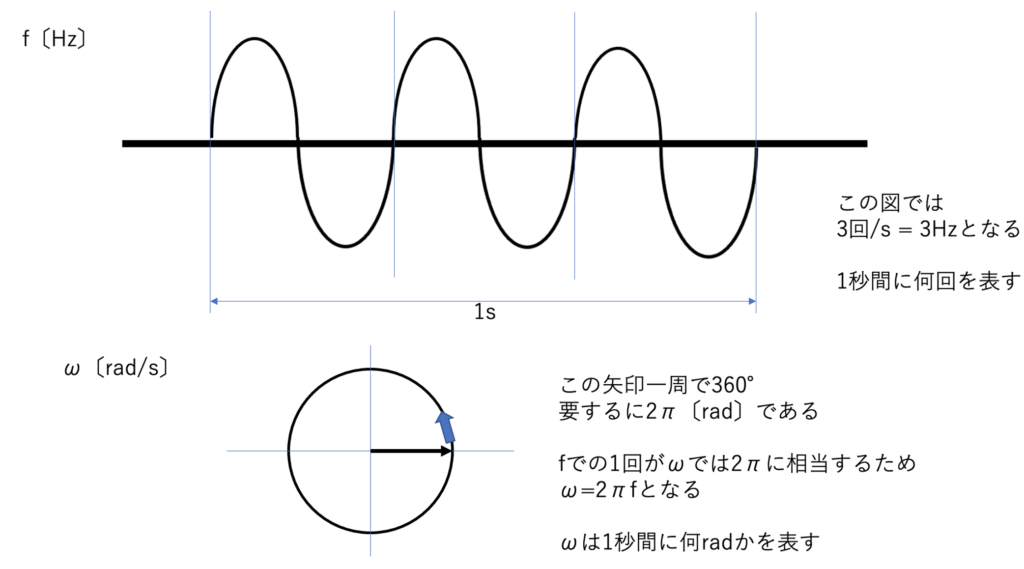
角周波数
ラーモアの方程式はω=γB0で表されますが周波数で表すとω=2πfとなります。
fは周波数です。
周波数Hzとは1秒間に何回繰り返すかを表します。→回/s
角周波数は1秒間に何radかを表しています。→rad/s
過去問からの出題
第5回-1
第5回-1
ω0 = γΒ0で表される関係について、正しい記述を選択してください。
a.磁気共鳴現象の基本を示し、ラーモア方程式とよばれる。
b.ω0は角振動数を表し、単位は 1/rad である。
c.γは磁気回転比と呼ばれる比例定数である。
d.γは静磁場強度によって異なる値を持つ。
e.Β0は磁束密度を表し、単位は Wb/m2 である。
a.○です。
b.×rad/s
c.○です。
d.×核種固有、静磁場強度に依存せず1Hのγは42.58MHz/Tとなります。
e.○です。
第10回-12
第10回-12
第5回-1と同問
第11回-20
第11回-20
第5回-1と同問
まとめ
ラーモアの方程式 ω = γB0
γは核種固有の値で磁場強度に依存しません。
γ = 42.6MHz/T *しゃにむに頑張る*・・・42.6、γ
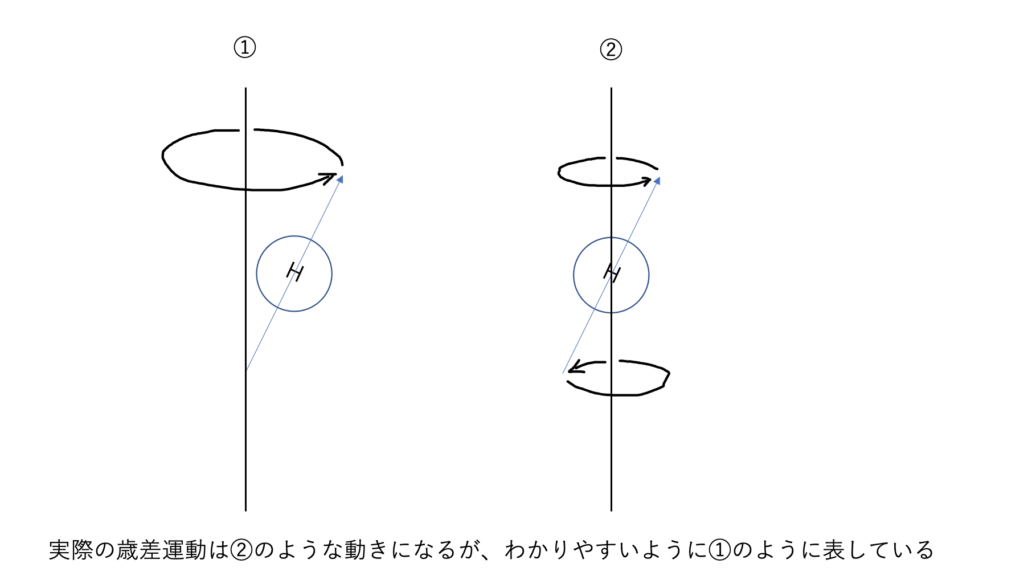
余談として、書籍でも何でも歳差運動を表す図は①の場合が多いと思いますがわかりやすいために用いられています。実際には②のようになります。
出題
参考書籍
MRI完全解説 P26
MRIの基本パワーテキスト P26











コメント