共鳴周波数幅とT2*(T2)

MT効果の原理や第５回-6でも出題されているのですが、共鳴周波数幅とT2*(またはT2)が反比例の関係となることについてです。

細かく説明すると長くなるので簡単に説明します。

式がかなり出てきますが、しっかり読む必要はないと思っています。

飽きそうだったら一気に「ここからがこの記事の重要なとこ！」に飛んでください。

用語

共鳴周波数幅はT2*(T2)値と反比例の関係がある。

解説

NMR信号

縦磁化に90°パルスを照射すると磁化Mは倒れxy平面を回転します。

横にコイルを設置すると、磁化Mが近づいたり遠ざかったりするために誘導起電力が発生します。

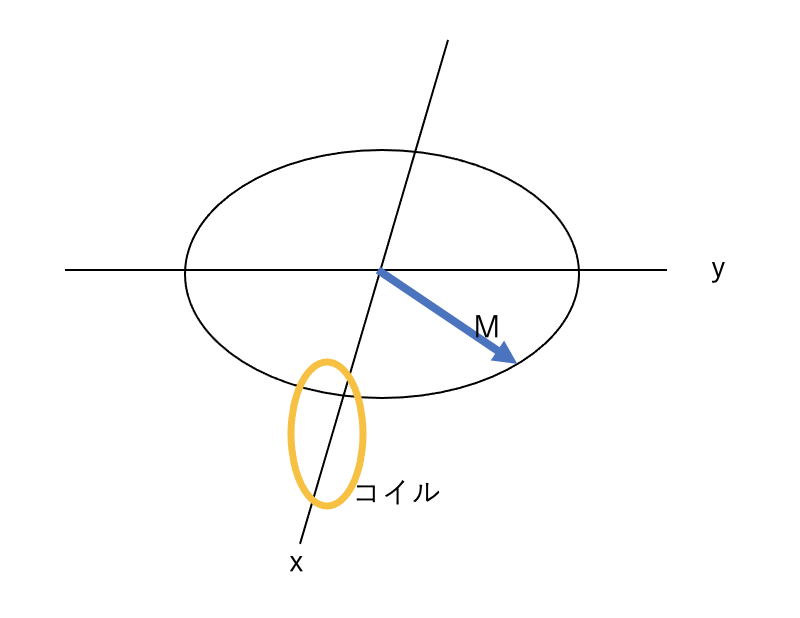
起電力V=dΦ/dt 　Φ：コイルを貫く磁束
V=AdM/dt Aは比例定数、磁化Mは単位面積あたりの磁束

この磁化Mの回転によって誘導された起電力がNMR信号となります。（実際には誘導電流）

Mはxy平面を角周波数ωで回転しますが各軸方向の成分は以下となります。

Mx=Msin(ω₀t)
My=Mcos(ω₀t)

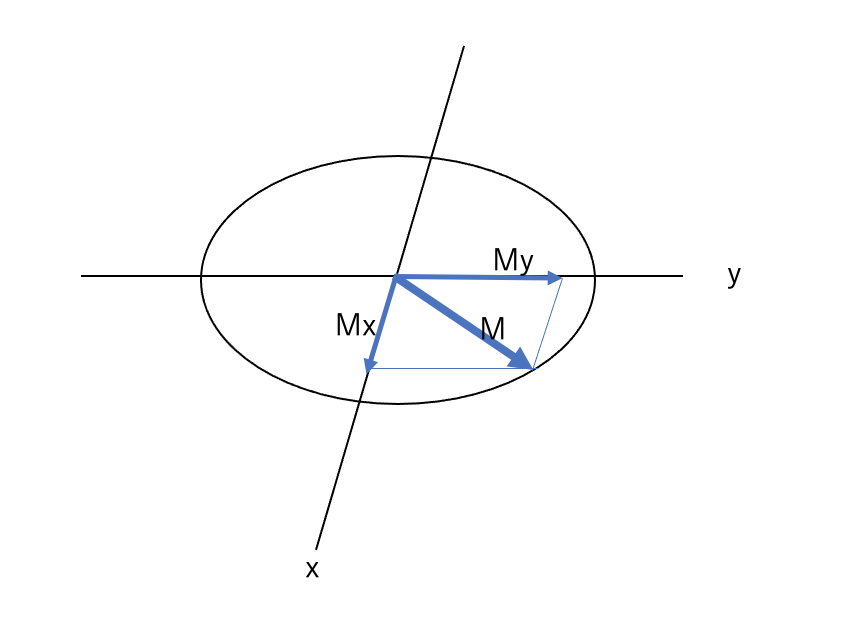
ここで、ベクトルMの大きさと位相(角度)を複素数で表示します。

(ベクトル)M=Mx+iMy
M=Mx+iMy=Msin(ω₀t)+iMcos(ω₀t)

これをV=AdM/dtに代入して

V=AdM/dt=AM(dsin(ω₀t))/dt+iAM(dcos(ω₀t))/dt
=AMω₀exp(-ω₀t)

Vx=AM(dsin(ω₀t))/dt=AMω₀cos(ω₀t)

Vy=AM(dcos(ω₀t))/dt=-AMω₀sin(ω₀t)

V=Vx+iVy

直角位相感受性検波

Vxの式、ω₀をωに変更、Aは比例定数なので書き直して

Vx∝M₀ωsinθ・cos(ωt)
Vx∝M₀ωcos(ωt)

信号Sxは

Sx∝M₀ωcos[(ω-ω₀)t]

これはNMR信号の周波数を知るために基準角周波数ω₀(1.5Tでは63.9MHz)を差し引いたものです。

余弦波は偶関数のため、ω＞ω₀とω＜ω₀を区別できません。

そこで90°(π/2)位相のずれた周波数で検波することとなります。

Sy∝M₀ωcos[(ω-ω₀)t-(π/2)]=M₀ωsin(ω-ω₀)t

S=Sx-iSy∝M₀ω₀cos[(ω-ω₀)t]+M₀ω₀isin[(ω-ω₀)t]
=M₀ω₀exp[i(ω-ω₀)t]

基準角周波数と位相をずらして検波した信号から、

S(t)=K{M₀ωcos[(ω-ω₀)t]+iM₀ωsin[(ω-ω₀)t]
=KM₀ωexp[i(ω-ω₀)t]

(ω-ω₀)=ω’として

S(t)=K(ω’+ω₀)M₀[cos(ω’t)+isin(ω’t)]
=K(ω’+ω₀)M₀exp(iω’t)

ω’とは基準角周波数ω₀に比べてとてつもなく小さいため(ω’+ω₀)をω₀として、

S(t)=KM₀[cos(ω’t)+isin(ω’t)]=KM₀exp(iω’t)

横緩和

ここまで緩和を無視してきましたが、横緩和を考慮します。

RFパルス後はT2*緩和するため、上記式のM₀をM₀exp(-t/T2*)として、

S(t)=KM₀exp(-t/T2*)[cos(ω’t)+isin(ω’t)]

ここからがこの記事の重要なとこ！

すみません、前置がかなり長くなりました。

ここまでのNMR信号は横軸を「時間」とする時間軸となっています。

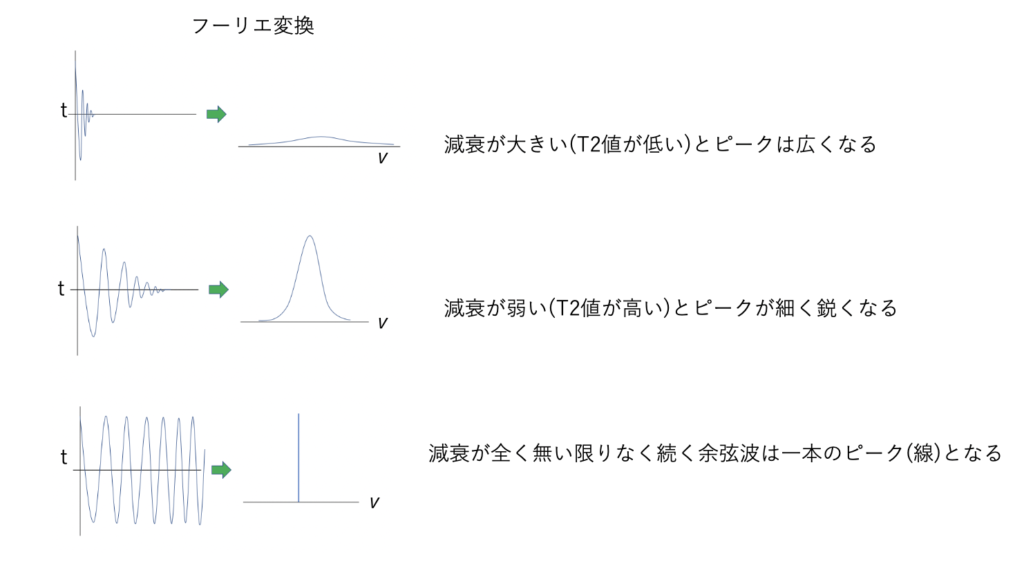
これをフーリエ変換することで横軸を「周波数」とする周波数領域となります。

そうすることで信号がどのような振幅と正余弦波で構成されているかが分かります。

前述の式、S(t)=KM₀exp(-t/T2*)[cos(ω’t)+isin(ω’t)]をフーリエ変換します。

F(ω)=∮S(t)exp(-iωt)dt
=KM₀∮exp(-t/T2*)[cos(ω’t)+isin(ω’t)]exp(-iωt)dt
=KM₀∮exp(-t/T2*)[exp(-iωt)]exp(-iωt)dt

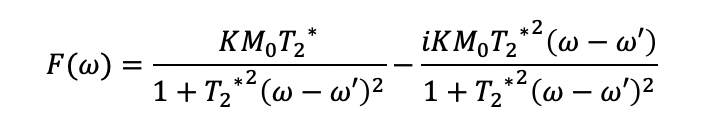
フーリエ変換の結果は上記となります。

実数部だけ取り出すと、ローレンツ関数となっています。

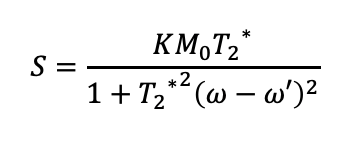
Sの最大値はω=ω’の時で、「KM₀T2*」となります。

S=KM₀T2*/2のように半値となるωをω₁とすると、

T2*²(ω₁-ω’)²=1
ω₁-ω’=±1/T2*

上記より

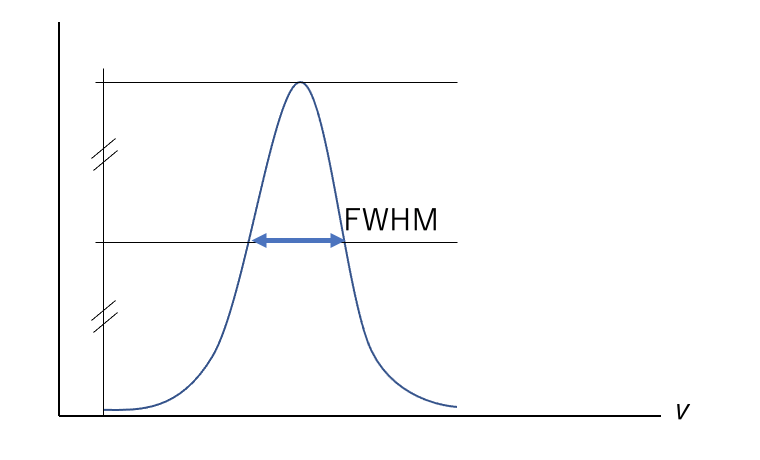
Δν=2|ν1-ν’|
=|ω₁-ω’|/π
=1/(πT2*)

これらより半値幅(FWHM)Δν=1/(πT2*)となり、

T2*が大きく信号が長く続くほど半値幅は狭くなり、細く鋭いピークとなります。

またT2*はT2にも置き換えられ、共鳴周波数幅と反比例の関係にあることが分かります。

まとめ

半値幅(FWHM)Δν=1/(πT2*)

なんかくどくどと長くなりましたが、共鳴周波数幅と反比例の関係であるということだけ抑えておけばいいんじゃないかと思います。

問題

5-(6) 磁気共鳴について、正しい文章を解答して下さい。

a. 1.5T の MRI 装置において、90°パルスの印加時間が 15ms であった場合、同じ出力の電磁波を用いて 180°パルスを印加するのに必要な時間は 30ms である。磁気モーメントは静磁場強度に比例するため、3.0T では 90ms の印加時間が必要である。
b. 横緩和時間は共鳴周波数幅に依存し、周波数幅は広いほど横緩和時間は延長する。
c. 縦緩和時間は静磁場強度と組織の相関時間に比例する
d. 常磁性物質が持つ不対電子の磁気モーメントはプロトンの磁気モーメントの 658 倍である。
e. 緩和効果は不対電子とプロトンの距離の 6 乗に比例する。

a.×
b.×周波数幅は広いほど横緩和時間は短縮
c.×比例しない
d.○
e.×距離に反比例